Из плоскости в пространство. Искусство замощения плоскости. Часть 2.
Переход 3D- 5DТворческая Лаборатория МастеровСакральная Геометрия 5-го измерения - от Лины Л.Технологии Нового Сознания - 5DМногомерная реальность
Опубликовано: 27 Апреля 2016
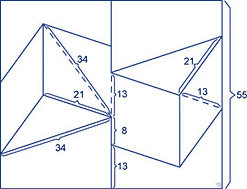
Чтобы исследовать и описать объём, люди пользуются способом проецирования объёмного тела на плоскости. Это выглядит примерно так:
Зная, как выглядят проекции, можно распознать, исследовать, сконструировать истинный трёхмерный объект.
Это и есть метод исследования, распространённый в классической кристаллографии. Исследователи изучают сначала одну проекцию или плоскость, «мостя её» просчитанными элементами плотно как паркет, и изучают при этом симметрию и другие особенности в замощённой плоскости.
Затем заполняют этими плоскостями весь трёхмерный объём, как книги заполняют кубическую упаковочную коробку. Этот метод так и называется - метод замощения.
Интерес к замощению возник в связи с построением мозаик, орнаментов и других узоров, основанных на правильных многогранниках: треугольниках, квадратах и шестигранниках.
Замостить плоскость из правильного пятиугольника или пентагона никогда не удавалось. Он оставляет прорехи - незаполненные щели. И поэтому, в классической кристаллографии пентагональная симметрия считается по сегодняшний день запрещённой.
И, наконец, такой способ был найден.
В 1976 году английский ученый математик Роджер Пенроуз, активно работающий в различных областях математики, общей теории относительности и квантовой теории, дал математическое описание, названной в честь него «мозаики Пенроуза».
Она позволила с помощью всего лишь двух плиток весьма простой формы замостить бесконечную плоскость никогда не повторяющимся узором.
Чтобы понять математическую сущность "ромбов Пенроуза", обратимся к пентаграмме.
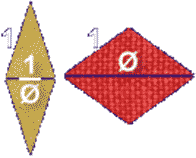
В своей простейшей форме "плитки Пенроуза" представляют собой набор ромбовидных фигур двух типов, одни с внутренним углом 36°, другие - 72°. Каждый состоит из двух треугольников, которые заполняют соответствующую модель пентаграммы.
Соотношения элементов пентаграммы полностью отражают золотую пропорцию Фибоначчи. Ее основой является иррациональное число = 1,6180339…
Идея Пенроуза о плотном заполнении плоскости с помощью "золотых" ромбов была трансформирована на трехмерное пространство.
При этом роль "ромбов Пенроуза" в новых пространственных структурах могут играть икосаэдры и додекаэдры.
Это была красивая находка, всего одна из многочисленных придумок светлого и цепкого ума Роджера Пенроуза, который увлекается пространственными парадоксами. Здесь присутствует его безукоризненое понимание золотой пропорции Фибоначчи, что приблизило его исследование к искусству.
И именно это послужило базой для дальнейших исследований и открытия квазикристаллов в химических лабораториях и новому, более творческому пониманию трёхмерного пространства, как для науки,так и для искусства.
Одной из ярких примеров творческого исследования, привлекших моё внимание, стала молодая словенская художница Матюшка Тейя Крашек.
Она получила степень бакалавра живописи в Колледже визуальных искусств (Любляна, Словения). Ее теоретическая и практическая работа фокусируется на симметрии как связующей концепции между искусством и наукой.
Ее художественные работы представлялись на многих международных выставках и опубликованы в международных журналах.
М.Т. Крашек на своей выставке ‘Kaleidoscopic Fragrances’, Любляна, 2005
Художественное творчество Матюшки Тейи Крашек связано с различными видами симметрии, плитками и ромбами Пенроуза, квазикристаллами, золотым сечением как главным элементом симметрии, числами Фибоначчи и др.
С помощью рефлексии, воображения и интуиции она пытается подобрать новые отношения, новые уровни структуры, новые и различные виды порядка в этих элементах и структурах.
В своих работах она широко использует компьютерную графику как весьма полезное средство для создания художественных работ, которое является связующим звеном между наукой, математикой и искусством.
Если мы выберем одно из чисел Фибоначчи (например, 21 см) для длины стороны ромба Пенроуза в этой ощутимо нестабильной композиции, мы можем наблюдать, как длины некоторых отрезков в композиции образуют последовательность Фибоначчи.
Большое количество художественных композиций художницы посвящено квазикристаллам Шехтмана и решеткам Пенроуза.
В этих удивительных композициях проявления круговой симметрии можно наблюдать отношения между ромбами Пенроуза:
каждые два соседних ромба Пенроуза образуют пентагональную звезду. Можно заметить Декагон, образованный ребрами 10 смежных ромбов Пенроуза, создающий новый правильный многогранник.
И на последнем рисунке бесконечное взаимодействие ромбов Пенроуза - пентаграммы, пятиугольники, уменьшающиеся к центральной точке композиции. Отношения золотой пропорции представлены многими различными способами в различных шкалах.
Художественные композиции Матюшки Тейи Крашек привлекли огромное внимание представителей науки и искусства.
Мозаика Пенроуза - великолепный пример того, как красивое построение, находящееся на стыке различных дисциплин, обязательно находит себе применение.
Если узловые точки заменить атомами, мозаика Пенроуза станет хорошим аналогом двухмерного квазикристалла.
Это поможет науке и искусству соединиться в творческом поиске, чтобы по - новому понять пространство, в котором мы живём.
При написании статьи частично использовались материалы из интернета:
-
ЗАМОЩЕНИЕ ПЛОСКОСТИ В ПРОСТРАНСТВЕ.
-
Бельгибаев А.С. http://www.gymnazd.ru/lncpbtla/%D0%97%D0%B0%D0%BC%D0%BE%D1%89%D0%B5%D0%BD%D0%B8%D0%B5+%D0%BF%D0%BB%D0%BE%D1%81%D0%BA%D0%BE%D1%81%D1%82%D0%B8+%D0%B2+%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%B5a/main.html